Difference Between Mean And Median

Difference Between Mean And Median

The major dissimilarities or difference between mean and median can be highlighted as follows:

1. Introduction

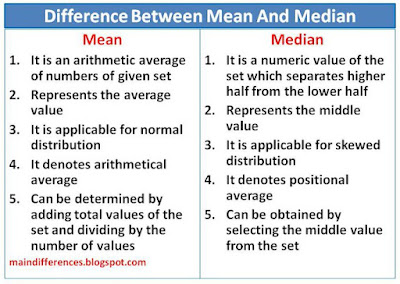
Mean: It is an arithmetic average of numbers of given set

Median: it is a numeric value of the set which separates higher half from the lower half

2. Represents

Mean: It represents the average value of a set of data

Median: It represents the middle value of the set of data

3. Applicable

Mean: It is applicable for normal distribution

Median: It is applicable for skewed distribution

4. Type Of Average

Mean: It denotes arithmetical average

Median: It denotes positional average

5. Calculation

Mean: It can be calculated by adding total values of the set and dividing by the number of values.

Median: Selecting the middle from the set (50% of the values should be less than median and other 50 % values should be greater than median.)

6. Example

Mean: 2,3,4,5,6,7,8,

Then, Mean = (2+3+4+5+6+7+8)/7 = 5

Median: 3, 4, 7, 8, 9

Then, Median = 7 because it exactly lies in the middle of set.

Mean Vs Median (Comparison Chart)

Basis	Mean	Median
Introduction	Arithmetic average of given set of numbers	Numeric value that separates higher half and lower half of set of numbers
Denotes/Represents	Average value	Middle value
Applicable For	Normal distribution	Skewed distribution
Type Of average	Arithmetic	Positional
Calculation	(Sum total of all values)     Number of values	Selection of middle value

I hope this post is helpful to understand the difference between mean and median and to make comparison between them.